- Titulní strana
- Úvod
- Pojmy a značení
- Soubory ke stažení
- 1. Úvod ke stereometrii
- 2. Základní věty
- 3. Určení přímky
- 4. Určení roviny
- 5.Vzájemné polohy
6.Polohové konstrukční úlohy
Vzájemná poloha tří přímek
Rozlišujeme devět vzájemných poloh tří přímek.
Abychom měli kompletní kapitolu o vzájemných polohách základních geometrických útvarů, přidáme ještě vzájemné polohy tří přímek, ačkoli ve středoškolských učebnicích se obvykle tato kapitola nevyskytuje.
Polohy, které bychom mohli také rozlišovat, jsou ty, kdy dvě přímky jsou totožné nebo všechny tři přímky jsou totožné. Tyto případy jsou však obsaženy v Kapitole 5.1.
Abychom nevynechali žádnou z možností vzájemných poloh tří přímek, tak vždy vezmeme jednu ze vzájemných poloh dvou přímek, Kapitola 5.1, a k nim budeme ve všech možných polohách přidávat přímku třetí.
Tranzitivnost rovnoběžnosti přímek
Pro tři přímky p, q, r platí: je-li p || q a současně q || r, potom i p || r.
Vzájemná poloha Průsečíky Číslo obrázku Značení Všechny tři rovnoběžné různé žádné obr. 1 (p || q)  (q || r)
(q || r)Dvě rovnoběžné různé, třetí s oběma různoběžná dva obr. 2 (p || q)  (p
(p r}
r}  (q
(q r)
r)Dvě rovnoběžné různé, třetí s jenou různoběžná a s druhou mimoběžná jeden obr. 3 (p || q)  (p
(p r)
r) (q
(q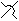 r)
r) Dvě rovnoběžné různé, třetí s oběma mimoběžná žádné obr. 4 (p || q)  (p
(p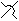 r)
r)  (q
(q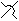 r)
r) Všechny tři různoběžné (pokud leží v jedné rovině mluvíme o svazku, pokud neleží, tak o trsu přímek) jeden obr. 5 (p  q)
q)  (p
(p r)
r)  (q
(q r)
r) Všechny tři různoběžné, každé dvě mají jeden průsečík tři obr. 6 (p  q)
q)  (p
(p r)
r)  (q
(q r)
r) Dvě různoběžné, třetí s oběma mimoběžná jeden obr. 7 (p  q)
q)  (p
(p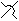 r)
r)  (q
(q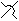 r)
r) Všechny po dvou mimoběžné žádné obr. 8 (p 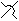 q)
q)  (p
(p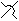 r)
r)  (q
(q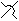 r)
r) Dvě mimoběžné, třetí s oběma různoběžná dva obr. 9 (p  q)
q)  (p
(p r)
r)  (q
(q r)
r)  Obr. 1
Obr. 1Všechny tři přímky jsou rovnoběžné, nemají žádný společný bod.  Obr. 2
Obr. 2Dvě přímky jsou rovnoběžné a třetí je protíná, dva průsečíky.  Obr. 3
Obr. 3Dvě rovnoběžné různé, třetí s jenou různoběžná a s druhou mimoběžná. 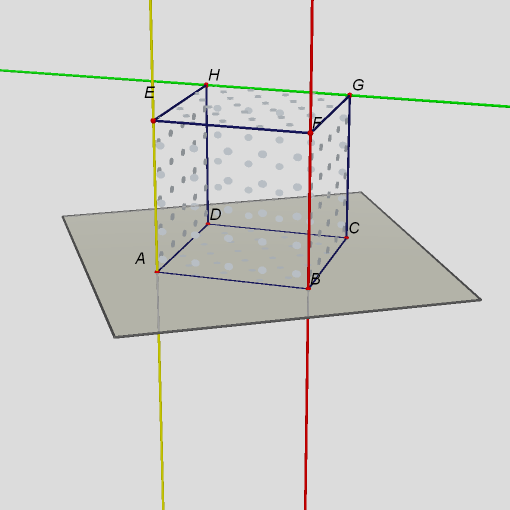 Obr. 4
Obr. 4Dvě přímky jsou rovnoběžné a třetí je s oběma mimoběžná. 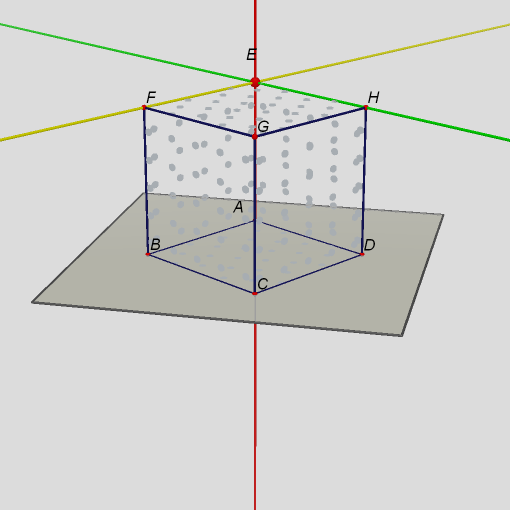 Obr. 5
Obr. 5Všechny tři přímky se protínají v jednom jediném bodě. 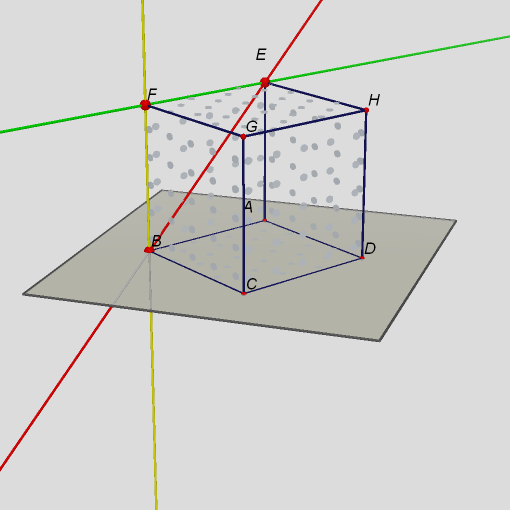 Obr. 6
Obr. 6Všechny přímky jsou navzájem různoběžné a to tak, že existují tři průsečíky. 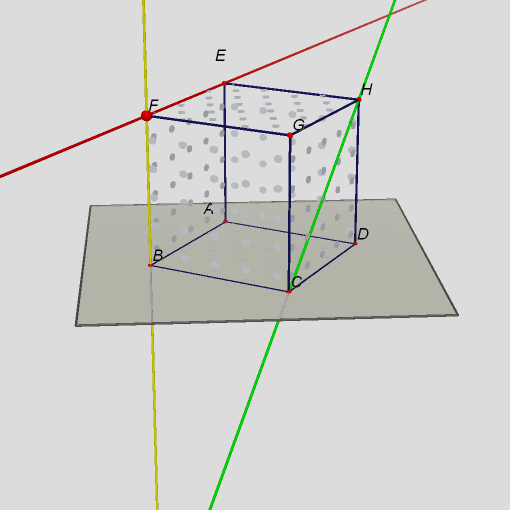 Obr. 7
Obr. 7Dvě přímky se protínají v jednom bodě a třetí přímka je k oběma mimoběžná. 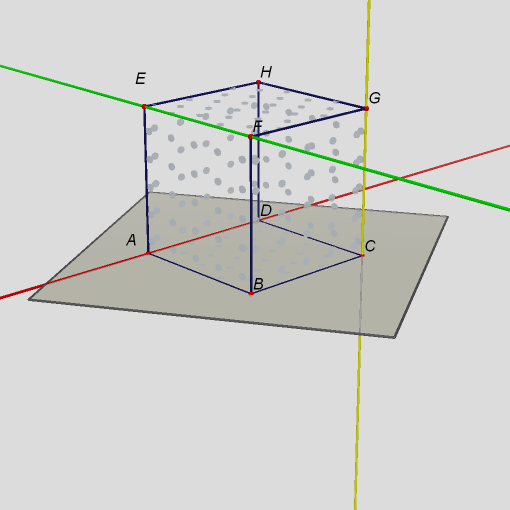 Obr. 8
Obr. 8Všechny tři přímky jsou po dvou mimoběžné, nemají žádný společný bod. 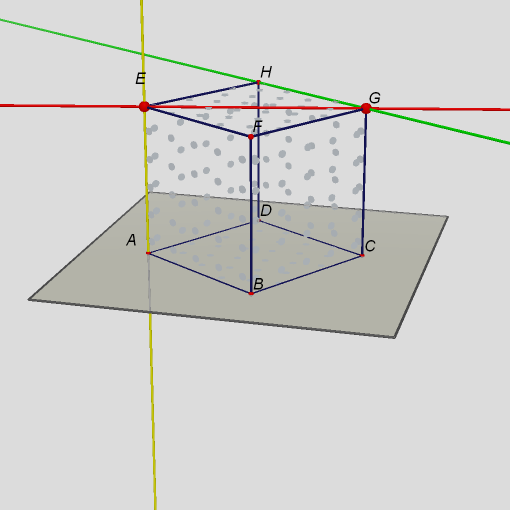 Obr. 9
Obr. 9Dvě přímky jsou mimoběžné a třetí přímka je protíná. Existují tedy dva průsečíky.
Úlohy
1. Na krychli ABCDEFGH jsou dány dvě přímky EH a BF. Určete k nim pomocí vrcholů krychle třetí přímku tak, aby existovaly dva průsečíky.
Řešením jsou přímky EF, HB, BE a HF.
Skryj výsledekZobraz výsledek2. Máme dánu krychli ABCDEFGH. Určete vzájemnou polohu přímek AD, BC a EF, určete společné body.
Přímky AD a BC jsou rovnoběžné různé, přímka EF je s oběma mimoběžná, nemají tedy žádné společné body.
Skryj výsledekZobraz výsledek3. Máme dánu krychli ABCDEFGH. Určete vzájemnou polohu přímek AC, GA a BF, určete společné body.
Přímky AC a GA jsou různoběžné, jejich průsečíkem je vrchol A, přímka BF je s oběma mimoběžná, nemá s nimi žádný společný bod.
Skryj výsledekZobraz výsledek4. Máme dánu krychli ABCDEFGH. Máme dány přímky HF a GE, určete pomocí vrcholů krychle třetí přímku tak, aby přímky měly tři průsečíky.
Řešením jsou přímky EF, FG, GH a HE.
Skryj výsledekZobraz výsledek5. Máme dán čtyřboký jehlan ABCDV. Body K, L, M jsou po řadě středy hran AB, BV a DV. Určete vzájemnou polohu přímek KV, LM a AD.
Přímky jsou po dvou mimoběžné, nemají žádný společný bod.
Skryj výsledekZobraz výsledek6. Máme dán jehlan ABCDV. Body K,L,M jsou po řadě středy hran AB, BC a CV. Určete k přímkám KL a BV třetí přímku pomocí dvou vrcholů tak, aby přímky měly dva průsečíky.
Řešením jsou přímky AB, BC a BD.
Skryj výsledekZobraz výsledek